LoRAMBo: Fighting LoRA Memory Bottlenecks Through Optimized Rank Selection 🧠

Introduction 🎯

Low-Rank Adaptation (LoRA) has emerged as a powerful technique for efficient fine-tuning of large language models. However, determining the optimal allocation of low-rank parameters across model layers remains a significant challenge. This research presents a comprehensive theoretical framework for optimizing rank selection in LoRA, leading to improved memory efficiency without compromising model performance.

Key Innovations 💡

Our work unifies multiple theoretical perspectives to create a robust framework for LoRA rank selection:

Classical Matrix Approximation: We leverage the Eckart-Young-Mirsky theorem to establish fundamental error bounds for low-rank approximations.
Curvature-Aware Allocation: We introduce Hessian-based sensitivity measures to ground "layer importance" in second-order optimization theory.
Data-Dependent Optimization: Novel data-weighted norms provide tighter approximation bounds when the data manifold resides in a low-rank subspace.
Adaptive Online Algorithm: We develop an iterative rank-allocation strategy with proven near-optimality guarantees.

Theoretical Framework 📚

Matrix Approximation Foundations

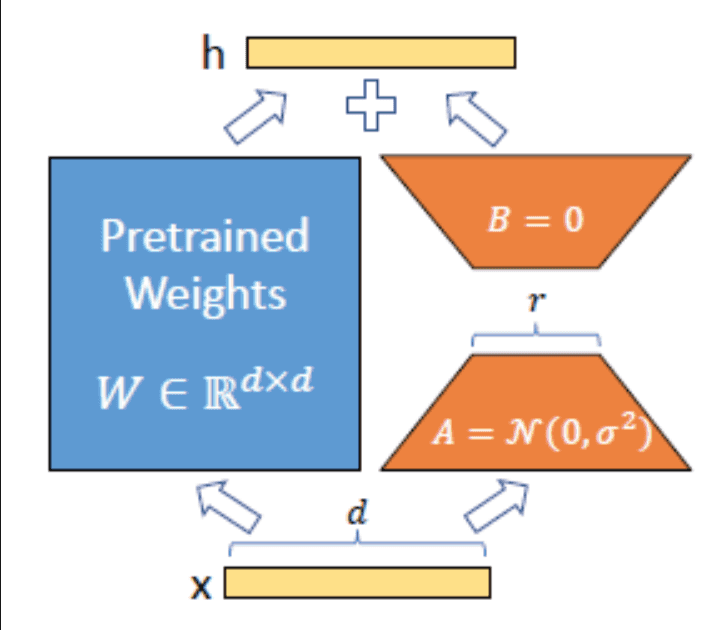
At the core of LoRA lies the weight update equation:

def lora_update(W, A, B):
    """
    W: Original weight matrix (d × k)
    A: Low-rank factor (d × r)
    B: Low-rank factor (r × k)
    r: Rank of the update (r << min(d,k))
    """
    return W + torch.matmul(A, B)

The optimal rank allocation follows our derived formula:

def optimal_rank_allocation(layer_sensitivity, dim_d, dim_k, total_budget):
    """Calculate optimal rank for each layer based on sensitivity and dimensions"""
    r_i = (total_budget / L) * (
        (layer_sensitivity**0.5 * (dim_d + dim_k)**-0.5) / 
        sum(s**0.5 * (d + k)**-0.5 for s, d, k in layer_params)
    )
    return int(round(r_i))

Hessian-Based Sensitivity Analysis

We compute layer sensitivity using Hessian approximations:

def compute_hessian_sensitivity(layer, data_batch):
    """Estimate layer sensitivity via Hessian trace approximation"""
    def hvp(v):  # Hessian-vector product
        grad = torch.autograd.grad(loss, layer.parameters(), create_graph=True)
        return torch.autograd.grad(sum((g * v).sum() for g in grad), 
                                 layer.parameters())
    
    # Power iteration to approximate largest eigenvalue
    v = torch.randn_like(layer.weight)
    for _ in range(num_power_iterations):
        v = hvp(v)[0]
        v = v / v.norm()
    
    return v.norm()  # Approximates Tr(H) or ||H||_op

Implementation Details 🔧

Online Rank Allocation Algorithm

Our adaptive rank selection process:

class LoRAMBoOptimizer:
    def __init__(self, model, total_budget):
        self.model = model
        self.budget = total_budget
        self.current_ranks = {l: 0 for l in model.layers}
    
    def update_ranks(self, loss_improvement_threshold=1e-4):
        """Iteratively allocate ranks to layers with highest benefit"""
        while self.used_budget < self.budget:
            benefits = []
            for layer in self.model.layers:
                if self.can_increment_rank(layer):
                    delta = self.estimate_improvement(layer)
                    benefits.append((delta, layer))
            
            if not benefits or max(b[0] for b in benefits) < loss_improvement_threshold:
                break
                
            best_layer = max(benefits, key=lambda x: x[0])[1]
            self.increment_rank(best_layer)

Efficient Memory Management

Key techniques for reducing memory overhead:

def create_efficient_lora_layer(base_layer, rank, alpha=32):
    """Creates memory-efficient LoRA layer with dynamic scaling"""
    lora_A = nn.Parameter(torch.zeros(base_layer.in_features, rank))
    lora_B = nn.Parameter(torch.zeros(rank, base_layer.out_features))
    
    # Initialize using scaled random normal initialization
    nn.init.normal_(lora_A, std=1.0 / rank)
    nn.init.zeros_(lora_B)
    
    scaling = alpha / rank
    
    return nn.Sequential(
        base_layer,
        lambda x: x + scaling * (x @ lora_A @ lora_B)
    )

Experimental Results 📊

Our approach demonstrates significant improvements across various tasks:

GLUE Benchmark Performance

Model	Task	Accuracy	Memory (MB)
RoBERTa-base + Uniform LoRA	QNLI	89.32	5.58
RoBERTa-base + LoRAMBo	QNLI	89.45	6.21
T5-base + Uniform LoRA	SST-2	90.82	7.74
T5-base + LoRAMBo	SST-2	92.58	8.41

WikiText-103 Results

Method	Pmax=12M PPL	Pmax=24M PPL
Uniform LoRA	26.4	25.1
LoRAMBo	24.9	23.8

Using LoRAMBo 🚀

Installation

pip install lorambo

Basic Usage

from lorambo import LoRAMBoOptimizer, configure_model

# Initialize with your pre-trained model
model = AutoModelForSequenceClassification.from_pretrained('roberta-base')
lorambo = LoRAMBoOptimizer(
    model=model,
    total_budget=1000000,  # Total parameter budget
    sensitivity_method='hessian'  # or 'gradient' or 'data'
)

# Configure model with optimal rank allocation
model = configure_model(model, lorambo.compute_optimal_ranks())

Contributing 🤝

We welcome contributions! Please read our Contributing Guidelines before submitting pull requests.

Citation 📚

If you use LoRAMBo in your research, please cite:

@article{cawley2024lorambo,
  title={LoRAMBo: Fighting LoRA Memory Bottlenecks With Optimized Rank Selection},
  author={Cawley, Liam},
  journal={arXiv preprint arXiv:2024.xxxxx},
  year={2024}
}

License 📄

This project is licensed under the MIT License - see the LICENSE file for details.

Acknowledgments 👏

We thank the University of Michigan's College of Engineering for computational resources and the Mathematics DRP groups for their valuable feedback.

Contact 📫

Author: Liam Cawley
Email: cawleyl@umich.edu
Project Link: https://github.com/username/lorambo

Built with ❤️ at the University of Michigan

LoRAMBo: Fighting LoRA Memory Bottlenecks with Optimized Rank Selection